Estrategias en los referéndums por la independencia

En los últimos tiempos ha habido un aumento del uso de la Teoría de Juegos para analizar negociaciones conflictivas, como las habidas entre el gobierno griego de Tsipras y la Troika o las del Brexit. En España se ha aplicado al análisis del procés. Uno de los aspectos importantes que se suele estudiar es la consistencia temporal de las acciones. Por ejemplo, Clara Ponsatí, a quien egoístamente me gustaría volver a ver cuanto antes en la vida académica, analizaba (aquí) las acciones tras una hipotética independencia de Cataluña: las amenazas por parte de España de vetar su incorporación a la UE no son creíbles porque, una vez independiente, estará en el interés de la propia España el que Cataluña sea un país próspero dentro de la UE. El análisis parte de una independencia de común acuerdo y sin tener en cuenta otras consideraciones como el efecto disuasorio para prevenir otros posibles procesos de independencia. El análisis de Ponsatí puede ser correcto, pero solo con esos supuestos. Si los cambiamos podemos llegar al resultado opuesto
.
Voy a intentar un análisis de consistencia temporal en otro aspecto de un proceso de independencia y lo haré en varios escenarios. No seré exhaustivo, así que si el lector advierte que falta incluir algún supuesto relevante no solo no me parecerá mal, sino que estaré encantado de ampliar el análisis incorporándolo.
Pongamos que una región, estado o comunidad autónoma, llamémosla CAT, quiere mayoritariamente separarse de un país, que llamaremos ESP. Sin embargo, la región no es homogénea: hay una provincia, BNA, en la que el deseo por la independencia no es mayoritario. ¿Qué podría pasar en un mecanismo de decisión sobre la independencia? Si las opciones son votar SÍ y votar NO a una independencia y si los resultados son la independencia de toda la región o su no independencia, el teorema de May nos dice que cada cual votará sinceramente. En consecuencia, CAT será independiente a pesar de que una parte no lo desee. Esta situación es poco interesante desde el punto de vista estratégico, como también es poco interesante el caso en que CAT no desea mayoritariamente la independencia.
Añadamos el siguiente aspecto: si CAT vota SÍ y BNA vota NO, entonces CAT se hará independiente, pero sin BNA. En esta nueva situación, a pesar de que las opciones en la votación sean, como antes, SÍ y NO a la independencia, los resultados posibles son tres (independencia de toda la región, independencia de la región sin la provincia y no independencia), por lo que el teorema no se aplica. Es más, según el teorema de Gibbard–Satterthwaite ningún sistema de votación está libre de voto estratégico. Veámoslo ilustrado en tres procedimientos de decisión.
Lo primero es definir las preferencias del votante mediano de cada parte. Puede entenderse como el votante o grupo de votantes pivote, de cuyo voto depende que el resultado en la consulta sea uno u otro. Pongamos que estas preferencias son como las anotadas en la Tabla 1. En lo que sigue, CAT será toda la región menos BNA (implícitamente asumimos que el voto del grupo pivote en BNA no altera el total de CAT).
En la Tabla 1, “Independencia parte” significa que CAT es independiente, pero sin la provincia BNA, que se queda en ESP. Si en las preferencias de CAT “Independencia parte” fuera preferido a “No independencia”, en CAT la estrategia de votar SÍ en un referéndum sería mejor en cualquier caso y, sabido esto, en BNA también ganaría la opción SÍ. De nuevo, esta situación es poco interesante estratégicamente a la par que seguramente poco realista si BNA es una provincia muy poblada y que contiene a la capital política y económica. La columna “Valor” indica que para cada territorio la mejor opción vale 2, la siguiente vale 1 y la última, cero. Los números son irrelevantes, basta con que indiquen el orden de preferencia.
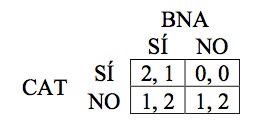
La Tabla 2 muestra el juego al que se enfrentan CAT y BNA en un referéndum. Cada parte (cada votante mediano) elige entre votar SÍ y votar NO. Si en ambos territorios sale SÍ se produce la independencia con todos los territorios. En este caso el votante mediano de CAT gana 2 y el de BNA gana 1. Si en CAT gana el SÍ y en BNA gana el NO la independencia se produce sin la provincia BNA. Las ganancias son 0 para el votante mediano en ambos territorios. Si en CAT gana el NO, no importa el resultado en BNA, puesto que no se producirá la independencia en ningún caso. El votante mediano de CAT gana 1 y el de BNA gana 2.
Este juego tiene dos equilibrios: en uno de ellos, en ambos territorios se vota SÍ, mientras que en el otro, ambos votan NO. Obsérvese que si cualquiera de los territorios anticipa que el otro vota SÍ, entonces tendrá todo el motivo para votar también SÍ. Con el otro equilibrio las cosas no están tan claras para BNA. Es cierto que si BNA anticipa que CAT votará NO, le da igual votar SÍ o NO, ya que en cualquier caso no habrá independencia. Pero si tiene alguna duda del resultado del referéndum en CAT, BNA hará mejor en votar SÍ. Anticipando esto, CAT votará SÍ. Esta manera de votar da un resultado favorable a la independencia en todos los territorios si las preferencias son las indicadas.
Si, en cambio, en BNA el votante mediano prefiere quedarse en ESP aunque el resto de CAT se independice, las cosas son distintas. Las siguientes tablas muestran las nuevas preferencias y el nuevo juego.
Si el mecanismo de decisión contiene un elemento temporal por el cual un territorio puede echarse para atrás tras saber el resultado del referéndum, tendríamos unos escenarios interesantes. Pongamos que primero vota CAT (toda la región) y luego, si gana el SÍ, BNA decide si mantenerse dentro de CAT o si se queda en ESP. En ese caso, BNA votará mantenerse en la nueva CAT independiente si sus preferencias son como en la Tabla 1 y no independizarse con CAT si son como en la Tabla 3. Anticipando esto, CAT votará SÍ en el primer caso y NO en el segundo.Ahora el único equilibrio es que ambos territorios voten NO. Es más, para BNA votar NO es estrictamente mejor si hay cualquier pequeña duda sobre el voto de CAT.
Si después del referéndum con resultado SÍ en toda CAT, pero NO en BNA, quien puede echarse para atrás es CAT, da igual cómo sean las preferencias de BNA, en BNA ganará el NO sabiendo que CAT no seguirá adelante con la independencia y, de esta manera, conseguirá su mejor resultado. La Tabla 5 resume las distintas posibilidades.
Algún lector tal vez se esté preguntando cuál es la decisión correcta, la que mejor refleja las preferencias de CAT y de BNA en cada caso. Malas noticias: no existe tal cosa como la decisión correcta. Hay maneras de decidir que llevan a distintos resultados y maneras que logran una mayor aceptación que otras.Según este análisis, lo que debería negociar ESP, con el apoyo de BNA, sería que CAT tuviera la última palabra. Frente a esto, tanto CAT como BNA intentarán mostrar que tienen las manos atadas una vez se haya hecho la votación, de manera que no habrá posibilidad de echarse atrás. En un escenario realista, sin embargo, parece que siempre será posible que CAT decida no optar por la independencia si BNA vota NO. Alternativamente, BNA deberá hacer creer a CAT que sus preferencias son como en la segunda tabla o, por lo menos, causar una duda lo suficientemente razonable para que el voto SÍ de CAT sea muy arriesgado.













Si metemos que existe la posibilidad de votar la independencia en las diferentes provincias de catalunya unilateralmente, también podemos meter la posibilidad de que pueda votar la independencia prácticamente cualquier región o grupo de personas.
Mismamente si a un grupo de personas les gusta-les beneficia la pederastia o la pedofilia o el tráfico de armas, drogas, personas, el cumplimiento estricto de la sharia etc, también se pueden sentir ya no solo muy molestos con el encaje legal español, sino también con el catalán y como a partir de ahí ya te puedes autoproclamar con capacidad de mantenerte al margen de las leyes vigentes y empezar a sacar las tuyas propias de la manga, pues el equilibrio de nash es mas bien de millones y millones de personas, pudiendo hacer lo que les de la gana simple y llanamente.
Obviamente el colectivo que mas capacidad tiene para hacer mas de lo que les de la gana a ellos y menos de lo que le de la gana al resto, es precisamente el mas capacitado militarmente y desde luego nuestros cruzados "catalanes" están peor en ese aspecto que hasta las organizaciones mafiosas mas inoperantes. Ósea que aunque España retirara completamente todos sus efectivos y dejara sin aplicación ninguna ley opresora española, lo último de lo último que iba a pasar es esa supuesta "voluntat d´un poble".
Los siguientes párrafos de tu comentario hablan de muchas posibilidades de autodeterminación. Que algunas de ellas sean absurdas o muy inconvenientes no dice nada sobre que lo sean otras. Pareces seguir el argumento de la pendiente resbaladiza: si empezamos concediendo esto, acabaremos concediendo todo. No tiene por qué ser así. Com sociedad, decidiremos unas cosas y no otras. Unos se dejarán llevar por unos argumentos, otros por otros. No se sigue que todos nos dejaremos llevar por el de la pendiente resbaladiza. Cada uno de los derechos y obligaciones de los que nos queramos dotar deberá ser analizado en su justo término, no en el de las exageraciones.
En mi caso, yo he querido aportar las dificultades para agregar las preferencias de los ciudadanos catalanes en un caso muy determinado, esperando que esto aporte algo al debate sobre la conveniencia de seguir reclamando el derecho de autodeterminación de Cataluña. Ni más ni menos.
Siento decir que los artículos de NeG alrededor del Procés están muy por debajo de nivel de calidad y relevancia que este blog ha tenido en asuntos como la crisis económica.
Es importante saber cómo pueden ser los finales, porque de ellos depende el análisis de las etapas anteriores en las negociaciones o en la gestión del conflicto. Una de las cosas que se pueden achacar al procés que hemos visto terminar, en términos estratégicos de la Teoría de Juegos, es que sus impulsores no tenían definidos los escenarios finales y, así todo, tenían como consigna seguir hasta el final. Esa es una estrategia que solo tiene sentido si (i) el final te favorece o (ii) tienes garantías de que no se llegará al final y que el proceso parará en una situación ventajosa para ti. Ninguna de estas dos condiciones se daba en el procés.
Lamento que consideres que los artículos sobre el procés en Nada es Gratis no estén a la altura de otros. Es posible que sea porque no se pueden decir cosas con mucho detalle, dados los imponderables políticos, porque este es un blog de Economía (y Teoría de Juegos, si me lo permiten mis colegas) y por tanto muchos aspectos del procés se quedan fuera de nuestro ámbito, porque estemos acostumbrados a análisis demasiado contundentes en la parte política y el análisis sosegado y parsimonioso que podamos hacer desde aquí choque con esa costumbre, o por múltiples otras razones que pueda haber. Seguiremos analizando e intentándolo, pero será despacio, como toca en ciencia y en conciencia.
Aunque el monopolio de la violencia español le concediera a cataluña cualquier cosa, mientras la comunidad autónoma de cataluña no tenga un monopolio de la violencia sobre ese territorio (cosa que no tiene y está en la antípodas de tener) lo que decidan o no decidan los catalanes es del todo irrelevante. Siendo mucho mas importante y relevante lo que decida o no la camorra italiana, la mafia rusa, el isis, al qaeda o absolutamente cualquiera que por a o por b se quiera unir a la fiesta (países extranjeros, mafias de cualquier tipo etc).
Mismamente el pueblo sirio incluso como país puede decidir sobre muchísimas cosas, pero obviamente a las células del isis, a los señores de la guerra, a los países extranjeros que están metidos en el conflicto, a las mafias locales, a Bashar al-Ásad y a su ejército y a cualquier que le venga en gana, les importan mas bien poco sus decisiones porque no tienen ningún monopolio sobre la violencia en esa zona que vaya a hacer que lo que decidan (o no) se vaya a llevar a la práctica.
Aunque la teoría de juegos de sus votaciones podría llevar a x o z resultados, la realidad va a ir por otro lado muy pero que muy divergente. Por muy resbaladizo que te resulte argumentalmente.
Por supuesto, tienes razón en que posiblemente se pudieran haber escrito más cosas sobre el tema.